This work presents a general monolithic formulation of steady fluid-structure interaction problems. I considered an incompressible flow and an elastic structure undergoing large displacements. The entire problem was solved in an implicit manner using a Newton-Raphson pseudo-solid approach. This approach allows the fluid and solid domains to be coupled using an elastic structure on which the fluid mesh lies. Thus, the formulation uses fluid velocity, pressure and pseudo-solid displacements as unknowns in the fluid domain and solid displacements in the solid domain. The equations are solved using an adaptive finite element method. The implementation is verified on a problem with a closed form solution obtained by the method of manufactured solutions. With this method, I can verify that the observed rate of convergence corresponds to the rate predicted by the theory. This powerful method allows verifying the implementation of the equations and validating the solution obtained by the solver.

Modeling an aneurysm and the glaucoma condition

I applied this method to model the mechanical behavior of an aneurysm under blood flow stresses. I modeled an elastic tube with a local wall weakness to mimic the presence of an aneurysm. I found that a flow recirculation forms in the cavity created by the weakness along with low wall shear stresses. This finding could explain the presence of plaque in aneurysmal tissues since low wall shear stresses are believed to trigger atherosclerosis and plaque formation. Also, I used a simplified model of an eyeball and apply an abnormally high intraocular pressure to mimic glaucoma. In these conditions, the lamina cribrosa induces stresses in the optical nerve, which leads to blindness. The computed deformations of the lamina cribrosa were in agreement with experimental data and thus showing the accuracy of the finite element model and solver.

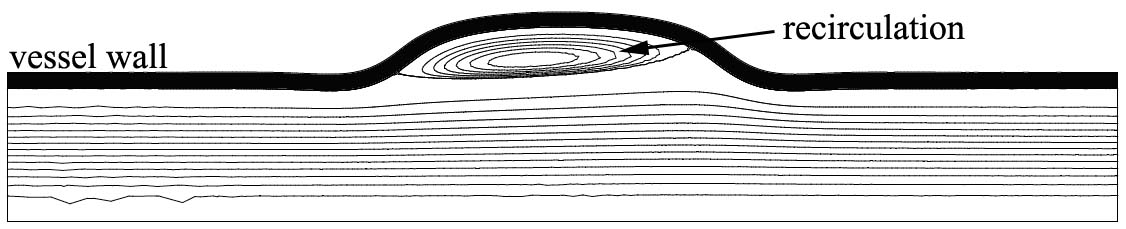
The wall weakness creates a cavity in which a flow recirculation forms.